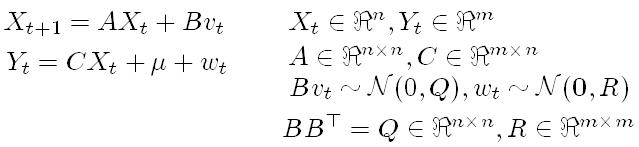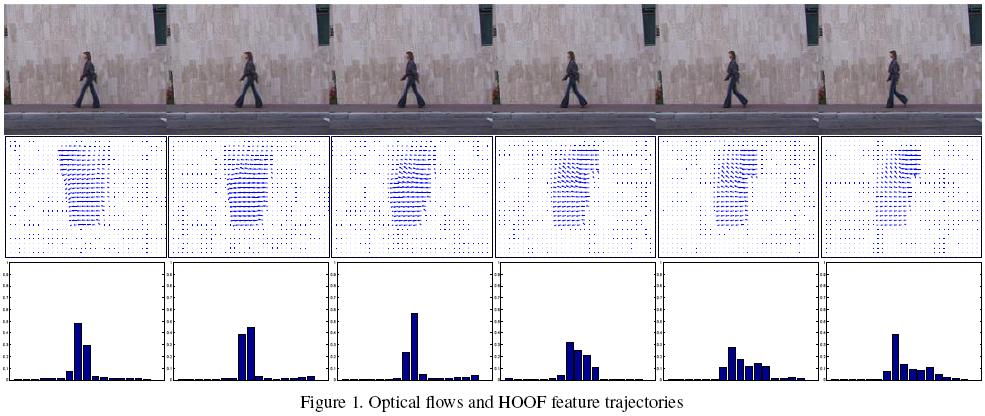
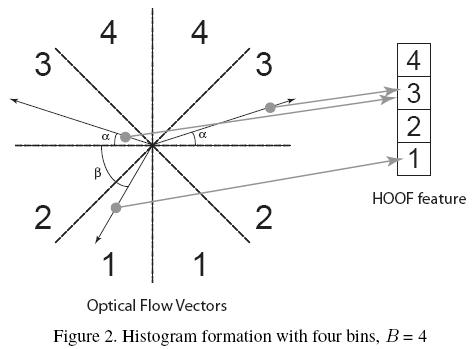
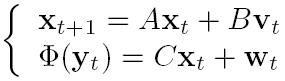
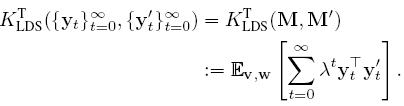
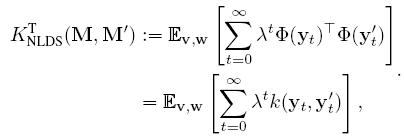
Once an affinity measure has been defined between two non-linear dynamical systems, we use k-Nearest Neighbors (k-NN) Classification. Also to perform more sophisticated classification, we can use kernel SVMs with the previously defined kernels.
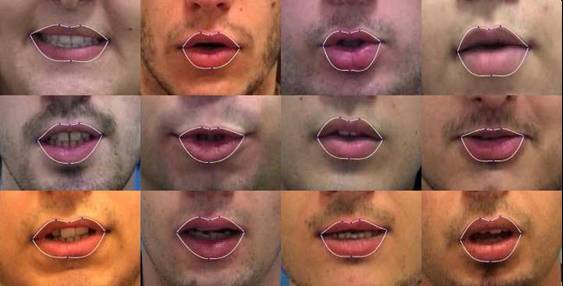
(a) Remove the natural head motion during the speaking act
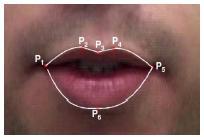
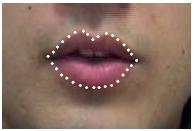
(b) Extract outer lip contours to collect six key-points on the lips and track these points throughout the video
(c) Interpolate from these six points to a total of 32 equi-distant points on the lip contours and record two types of features:
1. Landmarks - The coordinates of these points,
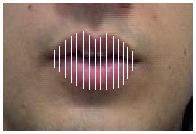
2. Distances - The distance between corresponding landmarks on the upper lip and the lower lip.
|
|
|
|
| Lip contours | Landmark features | Distance features |
|
|
1. N4SID
2. PCA-based suboptimal ID
| Finsler distance |
|
| Martin distance |
|
| Frobenius distance |
|
Another method for defining a measure of affinity between two LDS is through a kernel. The Martin Kernel, defined as:
| Martin kernel |
|
comes directly from the associated Martin Distance and is immediately computable from the subspace angles. Chan and Vasconcelos proposed another metric based on the Kullback-Leibler Divergence between the probability distributions of the outputs of the dynamical systems:
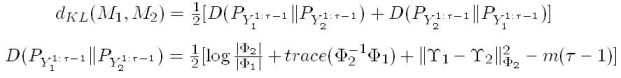
Vishwanathan et. al. introduced the family of Binet Cauchy kernels for the analysis of dynamical systems. One of these kernels, called the trace kernel between two ARMA model can be evaluated as:
![]()
Once an affinity metric has been defined between two linear dynamical systems, we use k-Nearest Neighbors (k-NN) Classification in the case of distances or k-Furthest Neighbors (k-FN) Classification for kernels. Also to perform more sophisticated classification, we use kernel SVMs with the previously defined kernels.
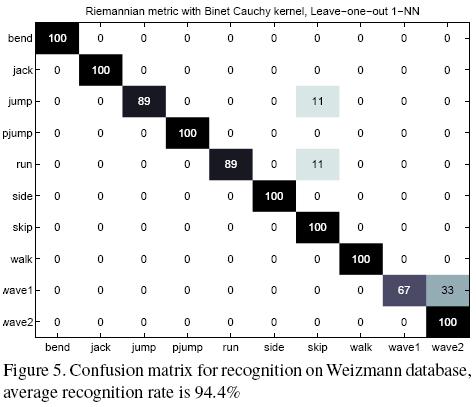
Groups - First row of the figure shows G4, the first 2 rows make up G8 and all the figures together represent G12.
The following table shows the classification errors of all groups in the name and digit
scenarios for landmark trajectories, L, using the PCA-based identification method, and using
both 1-NN classification with 5 different distances and SVM classification with
3 different kernels.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||