Simultaneous Estimation of an Object's Class, Pose, and 3D Reconstruction from a Single Image
Main Ideas
This project is based on the following three main ideas:
1- Thinking in 3D: Humans find remarkably easy to perceive three dimensional (3D) objects, even when presented with a single two dimensional image (e.g., when closing an eye or looking at a picture). This ability is essential to interact with the environment and to “understand” the observed images, which arguably can only be achieved when the underlying 3D structure of the scene is understood (see Fig. 1).

Figure 1: Examples of 2D images where the use of 3D prior knowledge is essential to understand the scene.
One ingredient contributing to the complexity of this task (of perceiving 3D objects in 2D images) is that it is inherently ambiguous, when no other constrains are imposed. Humans presumably solve it by relying on prior knowledge about the objects involved and the laws of nature that govern the physical interactions between objects and the creation of images. In this project we incorporate prior knowledge about different object classes by means of
3D Shape Priors. A 3D shape prior for a particular class encodes the probability that an object of the class, after being registered to a canonical pose, covers each point in 3D space (see Fig. 2).
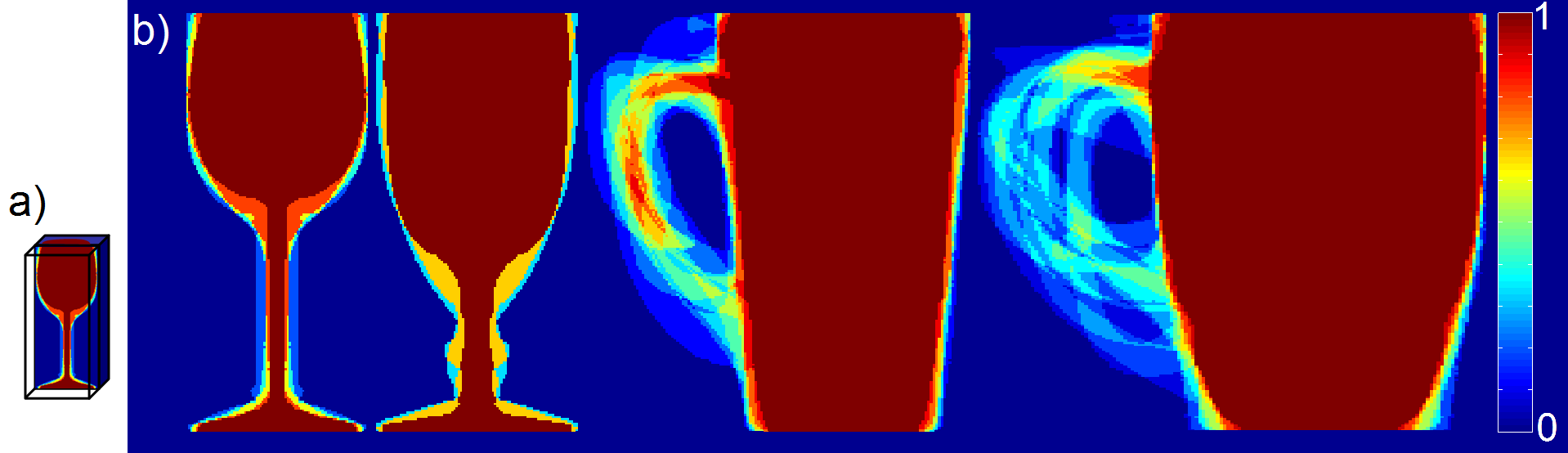
Figure 2: 2D cuts of different 3D shape priors along vertical planes (a), for the classes cups and mugs (b). Two different subclasses of each class are shown. The color of each point indicates the probability that the point would be inside an object of the class (see color bar to interpret the colors).
2- Looking at the shape: While in many cases a great deal of information about the class of an object can be obtained from the object's appearance (
i.e., texture), there are other cases where appearance is not a good indicator of the object's identity, and shape might be a more informative cue (see Fig. 3). For example, people may change clothes, paint their faces, or camouflage their cars, but the 3D shape of people and cars hardly changes because of that. Though appearance and shape cues are in general complementary, in this project we only condider prior knowledge about the shape of objects (encoded in the 3D Shape Priors mentioned above).

Figure 3: Appearance (left) can be deceiving, since it can be changed (purposely or not) to hide the identity or class of the object. Shape (right), in contrast, is more difficult to camouflage. And in some cases it provides enough information not just to distinguish the class of the objects in the scene, but also the activities they are performing.
3- Solving disparate tasks toghether: Most existing approaches in computer vision target a single specific task, such as object classification, pose estimation, tracking, segmentation or 3D reconstruction. In general, however, complex agents such as humans or robots need to solve many of these tasks. For example, a robotic manipulation system might need to not only identify an object, but also obtain a 3D reconstruction of it prior to manipulating it. Likewise, an airport surveillance system might need to detect that a person has left an object and then be able to estimate the dimensions and shape of the object, and track the person. While it would be possible to solve these tasks sequentially using existing approaches, we argue that there is no sensible order in which this should be done.
For instance, the fact that objects of a particular class tend to appear in certain locations (e.g., mugs tend to sit on the table, while trash cans usually sit on the floor), suggests that knowing the class of an object would be helpful to estimate its pose. Hence, classification would seem to precede pose estimation (class ⇒ pose). Conversely, because certain locations tend to contain particular classes of objects, knowing the pose of an object would be helpful to estimate its class (pose ⇒ class). In addition, to obtain the 3D reconstruction of an object from its 2D image using prior 3D shape knowledge about the class of the object (as argued above), we need to first determine which class shape prior to use (class ⇒ 3D reconstruction), and in order to use the prior knowledge in the appropriate parts of the scene, the object's pose needs to be estimated as well (pose ⇒ 3D reconstruction). Moreover, knowing the 3D shape of an object would allow us to discard object classes and poses that do not make physical sense, such as those where objects have invalid support (e.g., if they are levitating above the table), those where the objects do not have the right relative sizes, or those where objects intersect (hence, 3D reconstruction ⇒ pose, class).
Summary of the proposed approach
To implement these ideas we proposed a family of inference algorithms that we refer to as
self-conscious (SC) algorithms. SC algorithms are complementary to
Branch and Bound algorithms and are based on a
hypothesize-and-verify paradigm: multiple hypotheses are created, their log-probabilities are evaluated, and hypotheses are discarded as soon as they are proved worse (
i.e., their likelihood is lower) than some other hypothesis. In this project each hypothesis corresponds to a pair (Object Class, Object Pose) and thus finding the best hypothesis is equivalent to solving the classification and pose estimation problems (the 3D reconstruction is obtained as a by-product during the computation of the log-probability).
Since the number of hypotheses to consider could be potentially very large, and since the evaluation of each hypothesis' log-probability could be computationally very costly, it is essential to perform these evaluations very efficiently. To address these issues, we made use of two mechanisms. The first one is a
focus-of-attention-mechanism (FoAM) to sensibly and dynamically allocate the computational
budget among the different hypotheses to evaluate. This mechanism keeps track of the progress made for each computation cycle spent on each hypothesis, and decides on-the-fly where to spend new computation cycles in order to economically discard as many hypotheses as possible. The second mechanism is a
bounding mechanism (BM) which computes
lower and upper bounds for the log-probability of a hypothesis, instead of evaluating it
exactly. These bounds are in general significantly less expensive to evaluate, and they are obtained for a given computational budget (allocated by the FoAM), which in turn defines the tightness of the bounds (
i.e., higher budgets result in tighter bounds). In some cases, these inexpensive bounds are already sufficient to discard a hypothesis. Otherwise, these bounds can be efficiently and progressively refined by spending extra computational cycles on them (Fig. 4).
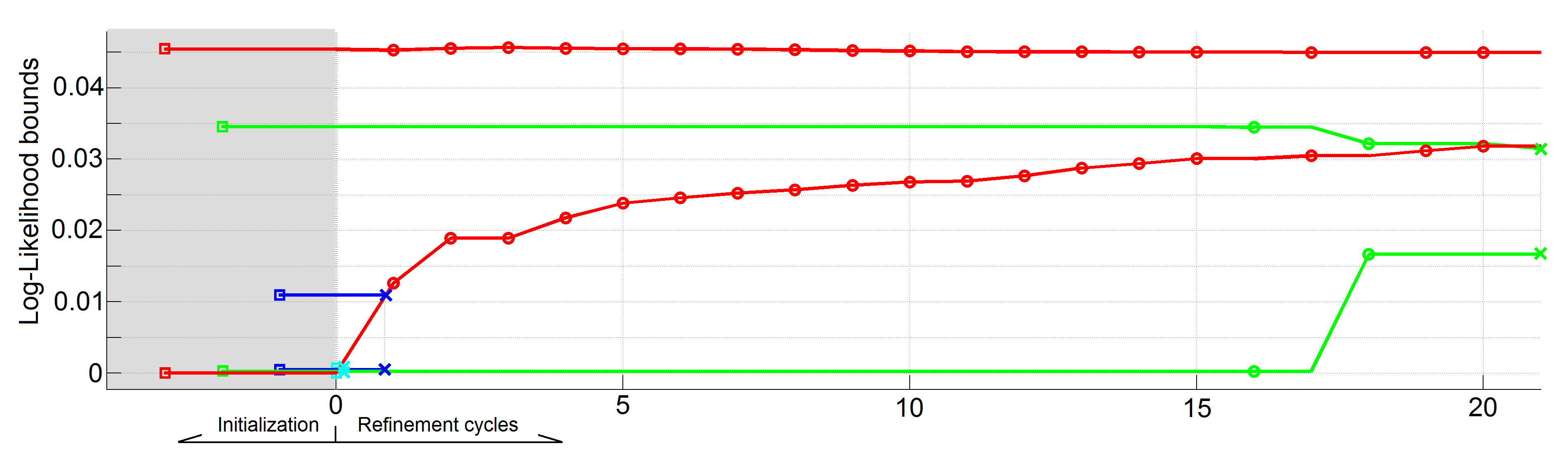
Figure 4: Progressive refinement of the hypotheses' log-probability bounds in a SC algorithm. The bounds of one hypothesis are represented by the two lines of the same color. Cycles in which the bounds of a hypothesis are refined are indicated by the marker 'o'. Hypotheses 3 (cyan) and 4 (blue) are discarded during the 1st refinement cycle. During the 21st cycle Hypothesis 2 (green) is discarded, proving that Hypothesis 1 (red) is optimal. Note that it is not necessary to compute exactly the log-probabilities to select the best hypothesis: the bounds are sufficient and much cheaper to compute.
SC algorithms are very efficient because the interaction between the FoAM and the BM results in that most hypotheses are discarded with very little computation (Fig. 5). Moreover, they are guaranteed to find the optimal solution, even in probabilistic graphical models with loops where other methods fail. Furthermore, they are guaranteed to find the
set of all optimal solutions, defined as those hypotheses whose log-probability's upper bound is greater than the maximum lower bound. This is a property that no other algorithm known to us can currently claim.
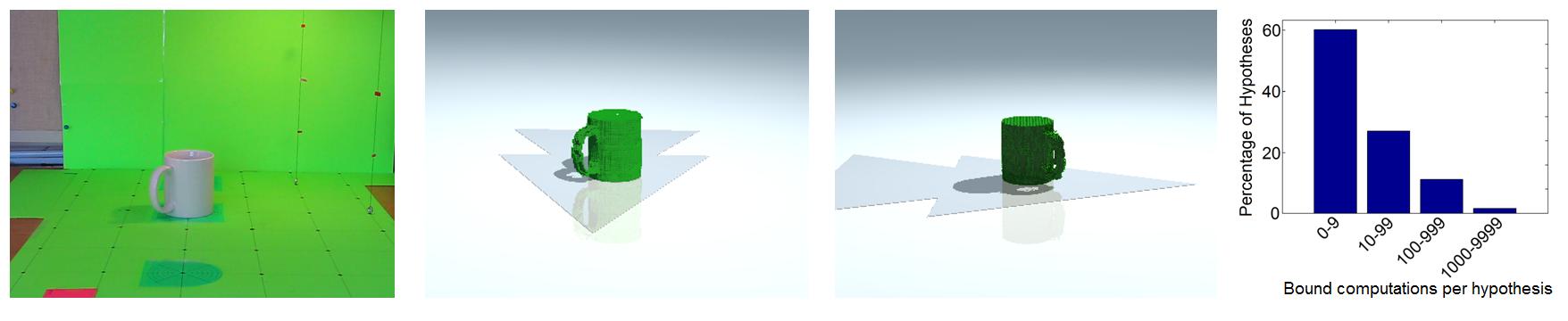
Figure 5: Summary of the results reported in [1]. Left: Original input image. Middle: Two views of the 3D reconstruction obtained for the input image. Right: Histogram of hypotheses grouped by bound pair computations spent on them. Note that very modest work is performed for most hypotheses (in particular 60% of the hypotheses were discarded with less than 10 bound pair computations).




