Manifold Clustering
Project Summary
Nonlinear dimensionality reduction refers to the problem of finding a low dimensional representation for a set of points lying on a nonlinear manifold embedded in a high dimensional space. This problem is fundamental to many problems in computer vision, machine learning and pattern recognition, because most datasets often have fewer degrees of freedom than the dimension of the data. In computer vision, for example, the number of pixels in an image can be rather large, yet most computer vision models use only a few parameters to describe the geometry, photometry and dynamics of the scene. The question of how to detect and represent low dimensional structure in high dimensional data is fundamental to many disciplines and several attempts had been made in the past in different areas to address this.

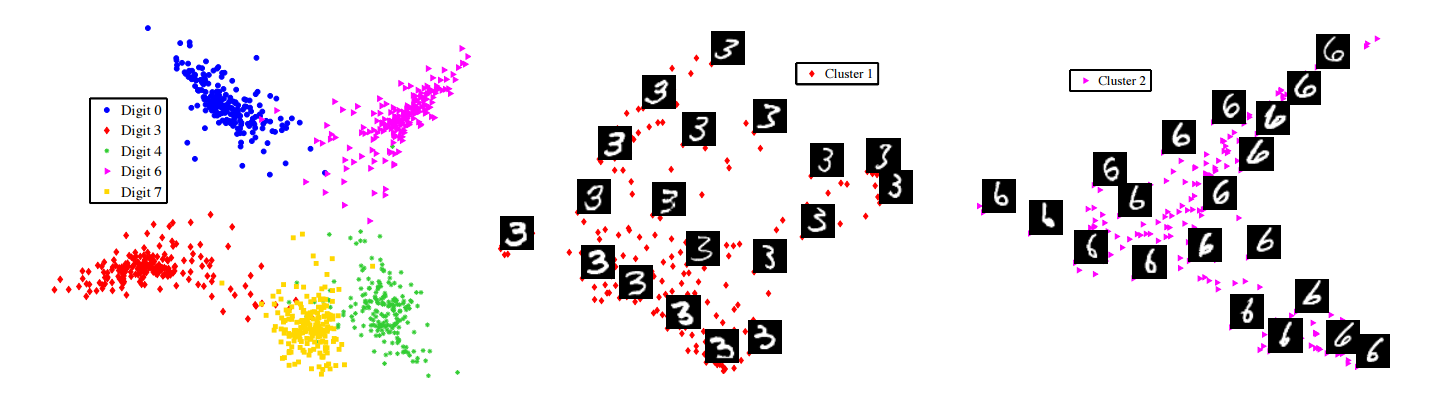
Over the past few years, various techniques have been developed for learning a low dimensional representation of a nonlinear manifold embedded in a high dimensional space. Although the goals of dimensionality reduction, classification and segmentation have always been intertwined with each other, considerably less work has been done on extending nonlinear dimensionality reduction techniques for the purposes of clustering data living on different manifolds. Unfortunately, most of these techniques are limited to the analysis of a single connected nonlinear manifold and suffer from degeneracies when applied to linear manifolds (subspaces). Figure 1 shows the types of manifolds to be segmentated into different groups.

Figure 1: Types of manifolds to be clustered.
locally linear manifold clustering
We address the problem of simultaneous nonlinear dimensionality reduction and clustering of data points drawn from multiple linear and nonlinear manifolds. We focus our investigation on the LLE algorithm, which compute a low-dimensional embedding from the eigenvectors of a matrix M that depends on local properties of the data. We show that if the data lives in a disconnected union of m connected manifolds, of which n &le m are subspaces of dimensions di, i=1...n, then the null space of M contains m eigenvectors that give the segmentation of the data and &sumi=1...n di eigenvectors that give the embedding coordinates for the subspaces. Therefore, in the case of nonlinear manifolds (n=0) the segmentation of the data can be obtained directly by looking at the null space of M. In the case of subspaces (n=m), contrary to intuition the situation is more difficult, because the nullspace of M contains both segmentation and embedding eigenvectors. We resolve this difficulty by showing that the variance of the segmentation eigenvectors is always smaller than that of the embedding eigenvectors. This leads to a new algorithm for clustering both linear and nonlinear manifolds by solving a generalized eigenvalue problem.

Application to Motion Segmentation
We apply our algorithm to the problem of segmenting multiple rigid-body motions in video. Given N point trajectories in F frames of a video sequence, the goal is to segment these trajectories according to m rigid motions. Depending on the camera projection models, these point trajectories lies on different manifolds. For affine cameras, there are m subspaces of dimensions 2, 3, or 4. For perspective cameras, there are m multilinear manifolds of dimension 3. Experiments on several sequences demonstrate that our algorithm is comparable to state-of-the-art computer vision algorithms. Please refer to this page for more details on motion segmentation.

Results for sequences with two and three motions
Two groupsTwo groupsThree groupsThree groups
Algorithm LLMC 5 LLMC 4n LLMC 5 LLMC 4n
Average 3.62% 4.44% 8.85% 11.02%
Median 0.00% 0.24% 3.19% 6.81%

Legend for the algorithms' naming scheme
LLMC 5Local Linear Manifold Clustering (projection to a space of dimension 5)
LLMC 4nLocal Linear Manifold Clustering (projection to a space of dimension 4 times the number of motions)

Work supported by startup funds from Johns Hopkins University, and by grants NSF CAREER IIS-04-47739, NSF EHS-05-09101 and ONR N00014-05-1083.
Publications
[1]
A. Goh and R. Vidal.
Segmenting Motions of Different Types by Unsupervised Manifold Clustering.
IEEE International Conference on Computer Vision and Pattern Recognition, June 2007.