Let {S₁, ..., S_n} be an arrangement of n linear subspaces of dimensions {d₁, ..., d_n} embedded in D dimensional space. Consider a given collection of N = Σ_i N_i data points {y₁, ..., y_N} drawn from the n subspaces. The sparse subspace clustering (SSC) algorithm [1], addresses the subspace clustering problem using techniques from sparse representation theory. This algorithm is based on the observation that each data point y ∈ S_i can always be written as a linear combination of all the other data points in {S₁, ..., S_n}. However, generically, the sparsest representation is obtained when the point y is written as a linear combination of points in its own subspace. A representation that uses other points from its own subspace is called subspace-preserving. In [1] we show that when the subspaces are low-dimensional and independent (dimension of the sum is equal to the sum of dimensions), subspace-preserving representation can be obtained by using L₁ minimization. The segmentation of the data is found by applying spectral clustering to a similarity graph formed using the sparse coefficients. More specifically, the SSC algorithm proceeds as follows.

Input: A set of points {y₁, ..., y_N} lying in a union of n subspaces {S₁, ..., S_n}.
1: Solve the sparse optimization problem min_C ||C||₁ s.t. Y = YC, diag(C) = 0, where C = [c₁, ..., c_N] is the matrix whose i-th column corresponds to the sparse representation of y_i using Y = [y₁, ..., y_N].
2: Normalize the columns of C as c_i ← c_i / ||c_i||_∞.
3: Form a similarity graph with N nodes representing the data points. Set the weights on the edges between the nodes by W = |C| + |C|^T.
4: Apply spectral clustering to the similarity graph.
Output: Segmentation of the data.

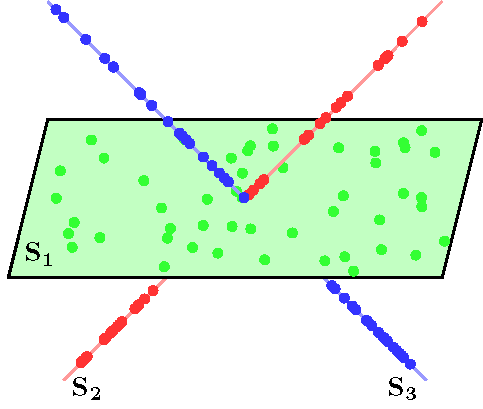
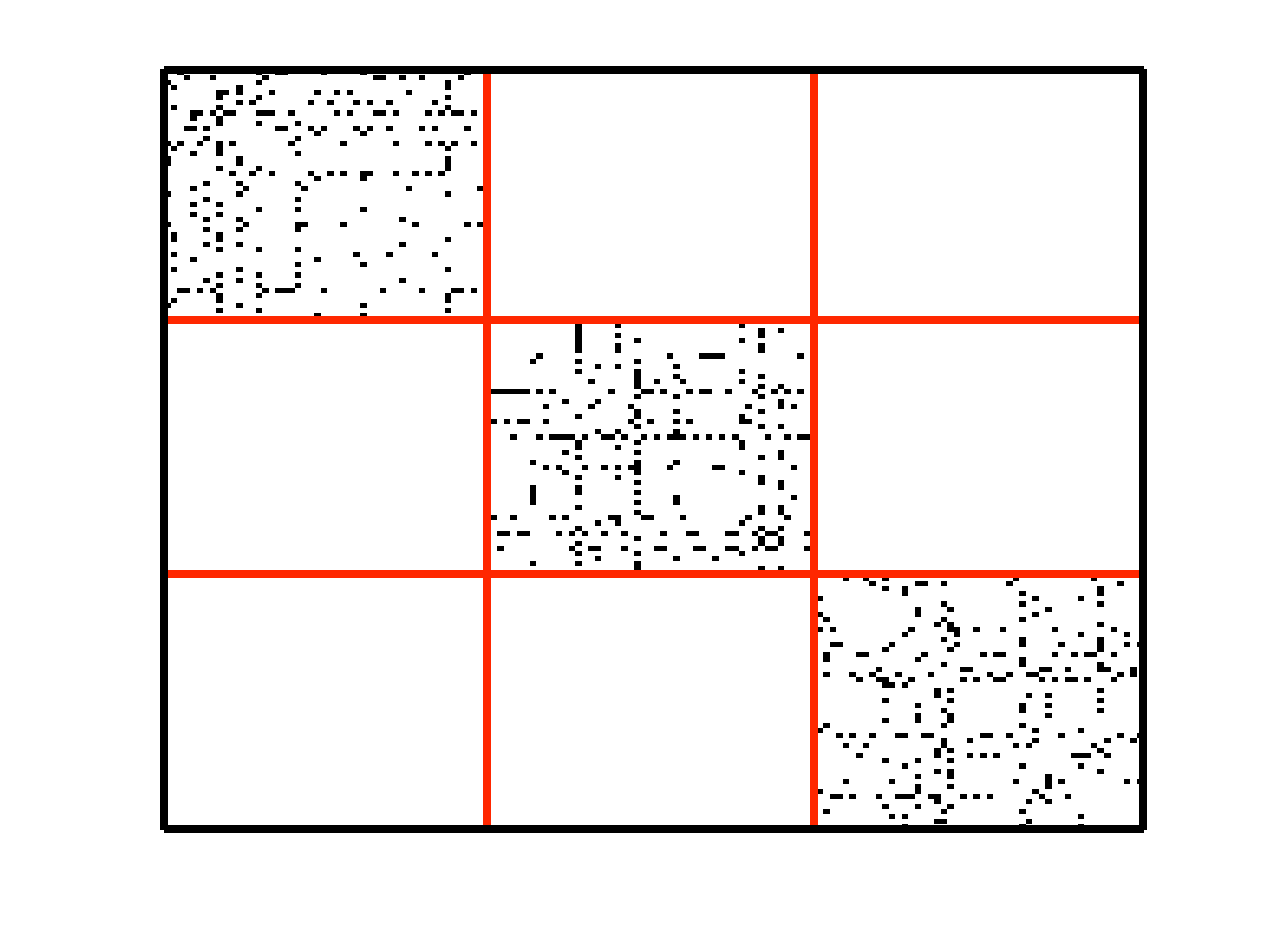
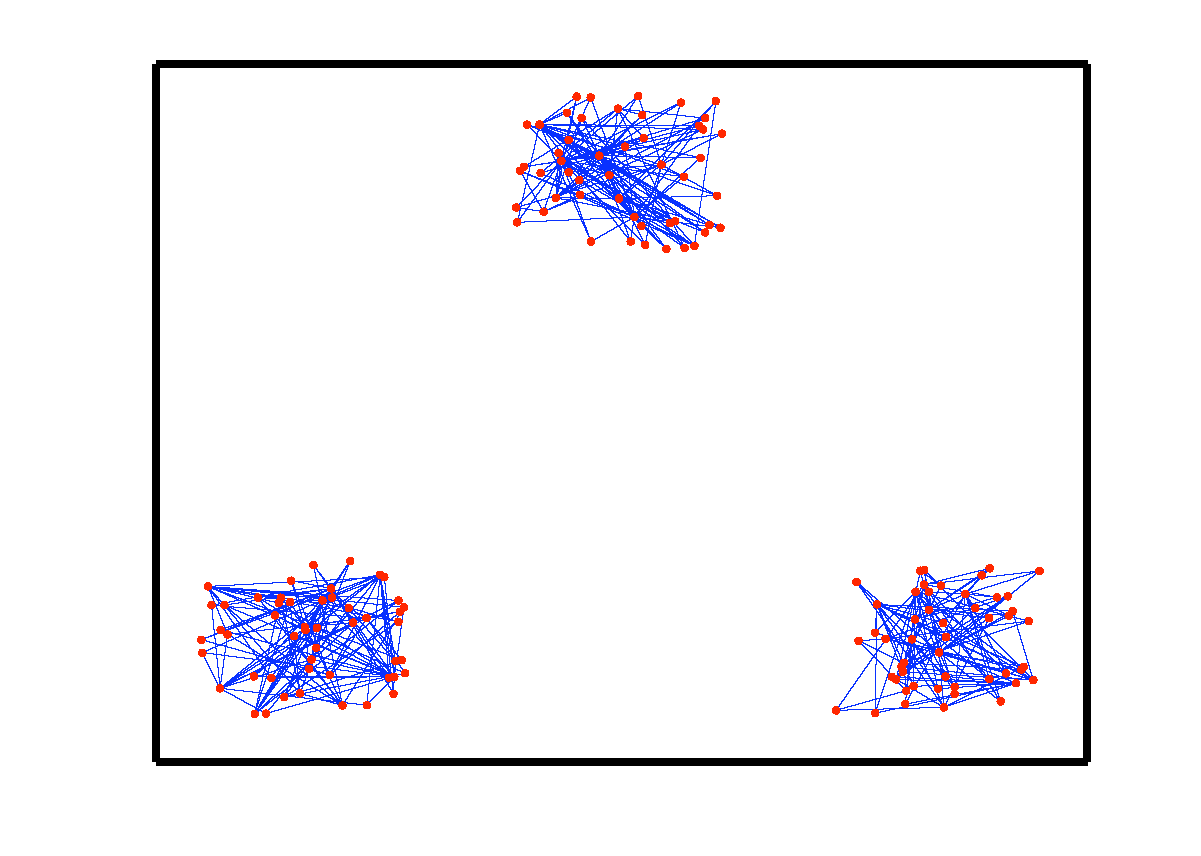
An example of data drawn from three subspaces and the corresponding adjacency matrix and similarity graph is shown in the figure below. For each data point, the L₁ minimization gives subspace-preserving representation, hence the adjacency matrix has a block-diagonal structure and the similarity graph has three connected components. Thus, using standard spectral clustering methods, we can recover the components of the similarity graph, hence the segmentation of the data.

Data drwan from 3 subspaces	Matrix of sparse coefficients	Similarity graph

However, requiring the subspaces to be independent is a strong assumption in practice. In [2], we address the more general problem of clustering disjoint subspaces (each pair of subspaces intersect only at the origin). We show that under certain conditions relating the principal angles between the subspaces and the distribution of the data points across all the subspaces, subspace-preserving representation can still be found by using convex L₁ optimization. This result represents a significant generalization with respect to the sparse recovery literature, which addresses the sparse recovery of signals in a single subspace. The subspace clustering problem is also much more challenging than block-sparse recovery problem, whose goal is to write a signal as a linear combination of a small number of known subspace bases. First, we do not know the basis for any of the subspaces nor do we know which data points belong to which subspace. Second, we do not have any restriction on the number of subspaces, while existing methods require this number to be large.

Dealing with noisy data
The SSC method shown in the Algorithm 1, is based on the assumption that the data are perfect (without noise) and lie on multiple linear subspaces. The algorithm can be modified to take into account noise in the data. When data points are contaminated with noise, we propose to solve the stable L₁ minimization problem by
where λ is a trade-off parameter between sparsity of the solution and the reconstruction error. A smaller value for λ favors sparsity while a larger value for λ results in a more dense coefficient vector but lower reconstruction error.

Dealing with missing entries
Classical SSC is not applicable to cases where the data is incomplete. In [6] we propose and evaluate two new approaches for subspace clustering and completion. The first one generalizes the sparse subspace clustering algorithm so that it can obtain a sparse representation of the data using only the observed entries. The second one estimates a suitable kernel matrix by assuming a random model for the missing entries and obtains the sparse representation from this kernel. Experiments on synthetic and real data show that the proposed algorithms are effective with each having advantages and disadvantages, as well as complementary strengths when compared to the basic approach of matrix completion followed by SSC.

Dealing with nonlinear manifold
While the linear model in SSC is a good approximation, in practice many datasets are better modeled by non-linear manifolds. By finding sparse representation of each data point using other data points that lie in a small neighborhood of it, the Sparse Manifold Clustering and Embedding constructs representation matrix that can effectively capture similarity of points lying in manifolds. By using the kernel trick, the Kernel Sparse Subspace Clustering can obtain a sparse representation of the data in a high-dimensional feature space. More details of these manifold clustering techniques are on this page.

Joint dimension reduction and clustering: Latent Space SSC
Computation of sparse representations in SSC is very computationally demanding especially when the dimension of the features is high. To deal with this problem, dimensionally reduction can be applied on the data prior to applying SSC. Motivated by some of the sparsity promoting dimensionality reduction methods, we propose a method for simultaneous dimensionality reduction and subspace clustering under the framework of SSC [4]. We learn the transformation of data from the original space onto a low-dimensional space such that its manifold structure is maintained:
where P is a matrix representing a linear transformation that maps signals from the original space to a latent output space. An efficient algorithm is proposed that simultaneously learns the projection and finds the sparse coefficients in the low-dimensional latent space.

Joint affinity learning and subspace clustering: Structured SSC
While SSC and the related approaches have been incredibly successful in many applications, a disadvantage is that they divide the problem into two separate stages: affinity learning and spectral clustering. Dividing the problem in two steps is, on the one hand, appealing because the first step can be solved using convex optimization techniques, while the second step can be solved using existing spectral clustering techniques. On the other hand, its major disadvantage is that the natural relationship between the affinity matrix and the segmentation of the data is not explicitly captured.
In [5], we propose a subspace structured norm on the self-expression coefficients matrix and turn the problem of subspace clustering into a unified optimization framework. Then, by integrating this norm with the standard L₁ norm, we propose a subspace structured L₁ norm and reformulate SSC into a unified optimization framework, termed as Structured Sparse Subspace Clustering, in which the separate two stages of computing the sparse representation and applying the spectral clustering are merged together automatically. We solve this problem efficiently via a combination of an alternating direction method of multipliers with spectral clustering.

While SSC is effective in dealing with small or medium size databases containing a few hundreds data points, large databases (beyond 10,000 data points) cannot be handled efficiently due to the high computation complexity in solving the L₁ minimization problems. Despite the recent advancement of scalable subspace clustering techniques, many of them adopt heuristics and pursue efficiency at the cost of lower accuracy. In this project, we advance scalable subspace clustering by pushing the boundary of the trade-off between efficiency and clustering accuracy. By using tools from sparse representation and convex optimization, the algorithms we developed are not only scalable but also theoretically guaranteed to correctly identify the subspaces.

SSC by orthogonal matching pursuit [7]
Orthogonal matching pursuit (OMP) is a well-known computationally efficient method for finding sparse representations. Subspace clustering by using OMP in lieu of the L₁ optimization in the original SSC for finding subspace-preserving representations is termed SSC-OMP. We show that SSC-OMP is orders of magnitude faster than the original SSC on synthetic as well as real databases, and can handle up to 100,000 data points. We also derive theoretical conditions under which the affinity produced by SSC-OMP is subspace preserving. Specifically, we show that SSC-OMP gives a subspace-preserving representation if the subspaces are independent, or else if the subspaces are sufficiently separated and the data is well distributed. Noticeably, these conditions are comparable with those derived for the original SSC.

Active set algorithm for Elastic net subspace clustering [8]
While the representation produced by SSC is guaranteed to be subspace-preserving under broad theoretical conditions, the affinity matrix may lack connectedness, i.e., data points from the same subspace may not form a connected component of the affinity graph due to the sparseness of the connections, which may cause over-segmentation. We investigate elastic net regularization (i.e., a mixture of the L₁ and L₂ norms) for scalable and provable subspace clustering. Firstly, an efficient and provably correct active set based algorithm is designed for solving the elastic net problem. The proposed algorithm exploits the fact that the nonzero entries of the elastic net solution fall into an oracle region, which we use to define and efficiently update an active set. The proposed update rule leads to an iterative algorithm which is shown to converge to the optimal solution in a finite number of iterations. Secondly, we also provide theoretical conditions under which the affinity generated by EnSC is subspace preserving, as well as a clear geometric interpretation for the balance between the subspace-preserving and connectedness properties.

Motion segmentation
We apply SSC to the motion segmentation problem, i.e., the problem of separating a video sequence into multiple spatiotemporal regions corresponding to different rigid-body motions in the scene. This problem is often solved by extracting a set of points in an image, and tracking these points through the video. Under the affine projection model, all the trajectories associated with a single rigid motion live in a low-dimensional subspace. Therefore, the motion segmentation problem reduces to clustering a collection of point trajectories according to multiple subspaces. We evaluate SSC on the Hopkins155 motion database, which is available online at http://www.vision.jhu.edu/data.htm. The database consists of 155 sequences of two and three motions which can be divided into three main categories: checkerboard, traffic, and articulated sequences. The following table shows the results of SSC as well as the state of the art on the Hopkins 155 database. The SSC algorithm achieves an average misclassification rate of 2.18% on the whole database, which is a significant improvement over the state of the art.

Algorithm	LSA	SCC	LRR	LRR-H	LRSC	SSC
Average	4.86%	4.10%	5.41%	2.56%	4.59%	2.18%
Median	0.89%	0.00%	0.53%	0.00%	0.60%	0.00%

Image clustering
We also test SSC and other clustering methods for clustering the MNIST database, which contains 70,000 images of handwritten digits 0 ~ 9. Note that the dataset is relatively large and many recent subspace clustering methods cannot be applied due to computation complexity and/or memory footprint issues. The SSC method achieves a good clustering accuracy and outperforms several baseline methods. However, SSC takes very long time to run, showing that it is inefficient in dealing with large databases. In contrast, SSC-OMP [7] and EnSC [8] are much more efficient than SSC while also achieve good clustering accuracy.

Algorithm	K-means	kNN-SC	NSN	SSC	SSC-OMP	EnSC
Misclassification rate	43.8%	14.8%	14.9%	7.6%	6.9%	6.0%
Running time (min.)	2	52	95	754	6	14

The Matlab code for SSC can be downloaded from the code webage.