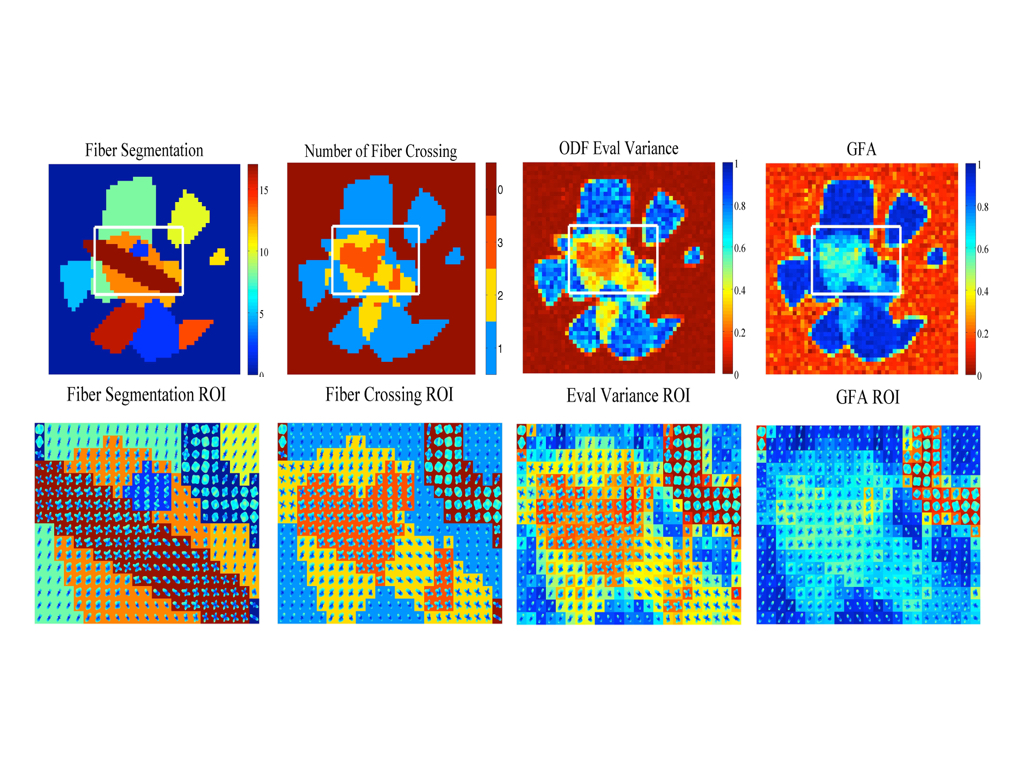
ODF Estimation
To estimate the orentation of fibers in each voxel of a HARDI brain dataset, orientation distribution functions (ODFs) are estimated from the HARDI signal. ODFs are probability distributions that live on the unit sphere and therefore must be nonnegative. Our work on ODF estimation enforces nonnegativity not only computationally on discrete grid points [1] but theoretically on the entire continuous spherical domain [2,3]. Enforcing nonnegativity is important for estimating accurate ODFs used for downstream processes of tractography, registration, segmentation and disease classification. In our most recent work, we consider that to enforce nonnegativity everywhere on a continuous domain, this equates to an infinite number of optimiztion contraints which is intractable. But even with a large number of constraints, many will be redudant. In fact, if we knew the minimum of the function, a priori, only one nonnegativity constraint at this point would suffice to enforce nonnegativiety everywhere. The work of [3] constructs an algorithm to select the optimal constraint needed to enforce ODF nonnegativity everywhere.
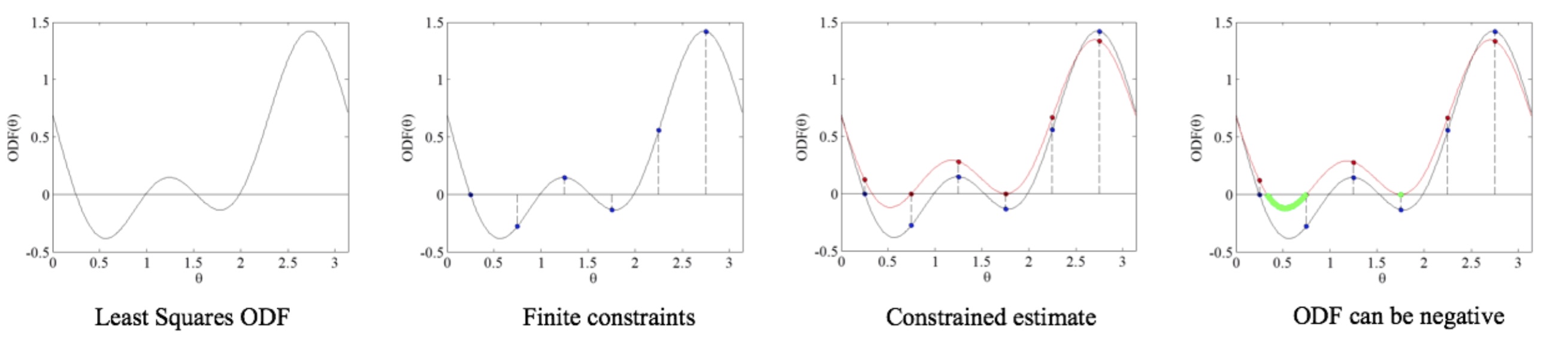
Figure 1: Illustration of nonnegativity enforcement on discrete set of points may leave continous functions negative. This calls for algorithms to enforce nonnegativity on the coninuous domain.

Figure 1: Illustration of nonnegativity enforcement on discrete set of points may leave continous functions negative. This calls for algorithms to enforce nonnegativity on the coninuous domain.